§ 1. Velocity of propagation of interaction

For the description of processes taking place in nature, one must have a system of reference. By a system of reference we understand a system of coordinates serving to indicate the position of a particle in space, as well as clocks fixed in this system serving to indicate the time.

There exist systems of reference in which a freely moving body, i.e. a moving body which is not acted upon by external forces, proceeds with constant velocity. Such reference systems are said to be inertial.

If two reference systems move uniformly relative to each other, and if one of them is an inertial system, then clearly the other is also inertial (in this system too every free motion will be linear and uniform). In this way one can obtain arbitrarily many inertial systems of reference, moving uniformly relative to one another.

Experiment shows that the so-called principle of relativity is valid. According to this principle all the laws of nature are identical in all inertial systems of reference. In other words, the equations expressing the laws of nature are invariant with respect to transformations of coordinates and time from one inertial system to another. This means that the equation describing any law of nature, when written in terms of coordinates and time in different inertial reference systems, has one and the same form.

The interaction of material particles is described in ordinary mechanics by means of a potential energy of interaction, which appears as a function of the coordinates of the interacting particles. It is easy to see that this manner of describing interactions contains the assumption of instantaneous propagation of interactions. For the forces exerted on each of the particles by the other particles at a particular instant of time depend, according to this description, only on the positions of the particles at this one instant. A change in the position of any of the interacting particles influences the other particles immediately.

However, experiment shows that instantaneous interactions do not exist in nature. Thus a mechanics based on the assumption of instantaneous propagation of interactions contains within itself a certain inaccuracy. In actuality, if any change takes place in one of the interacting bodies, it will influence the other bodies only after the lapse of a certain interval of time. It is only after this time interval that processes caused by the initial change begin to take place in the second body. Dividing the distance between the two bodies by this time interval, we obtain the velocity of propagation of the interaction.

We note that this velocity should, strictly speaking, be called the maximum velocity of propagation of interaction. It determines only that interval of time after which a change occurring in one body begins to manifest itself in another. It is clear that the existence of a

maximum velocity of propagation of interactions implies, at the same time, that motions of bodies with greater velocity than this are in general impossible in nature. For if such a motion could occur, then by means of it one could realize an interaction with a velocity exceeding the maximum possible velocity of propagation of interactions.

Interactions propagating from one particle to another are frequently called “signals”, sent out from the first particle and “informing” the second particle of changes which the first has experienced. The velocity of propagation of interaction is then referred to as the signal velocity.

From the principle of relativity it follows in particular that the velocity of propagation of interactions is the same in all inertial systems of reference. Thus the velocity of propagation of interactions is a universal constant. This constant velocity (as we shall show later) is also the velocity of light in empty space. The velocity of light is usually designated by the letter c, and its numerical value is

The large value of this velocity explains the fact that in practice classical mechanics appears to be sufficiently accurate in most cases. The velocities with which we have occasion to deal are usually so small compared with the velocity of light that the assumption that the latter is infinite does not materially affect the accuracy of the results.

The combination of the principle of relativity with the finiteness of the velocity of propagation of interactions is called the principle of relativity of Einstein (it was formulated by Einstein in 1905) in contrast to the principle of relativity of Galileo, which was based on an infinite velocity of propagation of interactions.

The mechanics based on the Einsteinian principle of relativity (we shall usually refer to it simply as the principle of relativity) is called relativistic. In the limiting case when the velocities of the moving bodies are small compared with the velocity of light we can neglect the effect on the motion of the finiteness of the velocity of propagation. Then relativistic mechanics goes over into the usual mechanics, based on the assumption of instantaneous propagation of interactions; this mechanics is called Newtonian or classical. The limiting transition from relativistic to classical mechanics can be produced formally by the transition to the limit $c \to \infty$ in the formulas of relativistic mechanics.

In classical mechanics distance is already relative, i.e. the spatial relations between different events depend on the system of reference in which they are described. The statement that two nonsimultaneous events occur at one and the same point in space or, in general, at a definite distance from each other, acquires a meaning only when we indicate the system of reference which is used.

On the other hand, time is absolute in classical mechanics; in other words, the properties of time are assumed to be independent of the system of reference; there is one time for all reference frames. This means that if any two phenomena occur simultaneously for any one observer, then they occur simultaneously also for all others. In general, the interval of time between two given events must be identical for all systems of reference.

It is easy to show, however, that the idea of an absolute time is in complete contradiction to the Einstein principle of relativity. For this it is sufficient to recall that in classical mechanics, based on the concept of an absolute time, a general law of combination of velocities is valid, according to which the velocity of a composite motion is simply equal to the (vector) sum of the velocities which constitute this motion. This law, being universal, should also be applicable to the propagation of interactions. From this it would follow that the velocity of

propagation must be different in different inertial systems of reference, in contradiction to the principle of relativity. In this matter experiment completely confirms the principle of relativity. Measurements first performed by Michelson (1881) showed complete lack of dependence of the velocity of light on its direction of propagation; whereas according to classical mechanics the velocity of light should be smaller in the direction of the earth’s motion than in the opposite direction.

Thus the principle of relativity leads to the result that time is not absolute. Time elapses differently in different systems of reference. Consequently the statement that a definite time interval has elapsed between two given events acquires meaning only when the reference frame to which this statement applies is indicated. In particular, events which are simultaneous in one reference frame will not be simultaneous in other frames.

To clarify this, it is instructive to consider the following simple example.

Let us look at two inertial reference systems $K$ and $K'$ with coordinate axes $XYZ$ and $X'Y'Z'$ respectively, where the system $K'$ moves relative to $K$ along the $X(X')$ axis (Fig. 1).

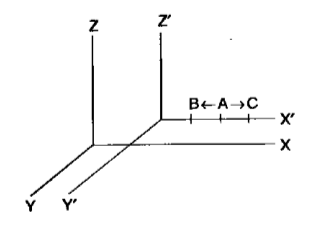
Suppose signals start out from some point $A$ on the $X'$ axis in two opposite directions. Since the velocity of propagation of a signal in the $K'$ system, as in all inertial systems, is equal (for both directions) to $c$ , the signals will reach points $B$ and $C$ , equidistant from $A$ , at one and the same time (in the $K'$ system)

But it is easy to see that the same two events (arrival of the signal at $B$ and $C$ ) can by no means be simultaneous for an observer in the $K$ system. In fact, the velocity of a signal relative to the $K$ system has, according to the principle of relativity, the same value $c$ , and since the point $B$ moves (relative to the $K$ system) toward the source of its signal, while the point $C$ moves in the direction away from the signal (sent from $A$ to $C$ ), in the $K$ system the signal will reach point $B$ earlier than point $C$ .

Thus the principle of relativity of Einstein introduces very drastic and fundamental changes in basic physical concepts. The notions of space and time derived by us from our daily experiences are only approximations linked to the fact that in daily life we happen to deal only with velocities which are very small compared with the velocity of light.