Binary indexed tree

Background

A Fenwick tree or binary indexed tree is a data structure that can efficiently update elements and calculate prefix sums in a table of numbers.[^1]

Space and Time Complexity

\[\begin{array}{lll} \text { Algorithm } & \text { Average } & \text { Worst case } \\ \text { Space } & \mathrm{O}(n) & \mathrm{O}(n) \\ \text { Search } & \mathrm{O}(\log n) & \mathrm{O}(\log n) \\ \text { Insert } & \mathrm{O}(\log n) & \mathrm{O}(\log n) \\ \text { Delete } & \mathrm{O}(\log n) & \mathrm{O}(\log n) \end{array}\]

Explaination

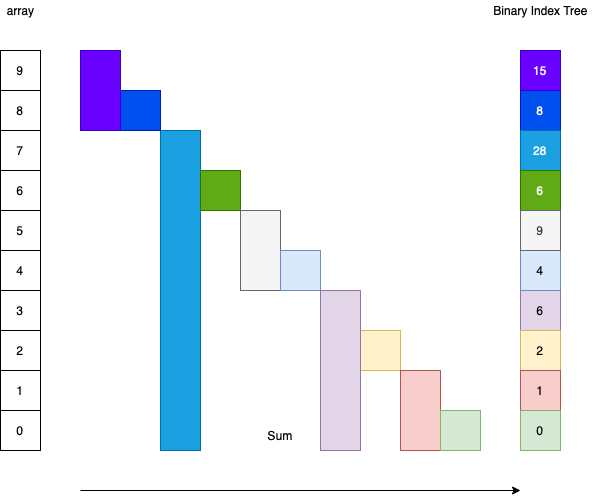
The picture show the data store in the binary indexed tree.

Supporse the name of original array is arr, the name of binary indexed tree is fenw. Than we have following relationship between arr and fenw.

fenw[0] = arr[0];
fenw[1] = arr[0] + arr[1];
fenw[2] = arr[2];
fenw[3] = arr[0] + arry[1] + arr[2] + arr[3];

Now, we need to found the pattern. First we are going to found out all index in fenw which contains arr[0]. The indexes are 0, 1, 3, 7, 15, ... . Now we see the pattern for arr[0]. First one is 0; second one is 1 which is 0 + 1 = 0 + pow(2,0); third one 3 which is 1 + pow(2,1) = 3, and so on. When we are starting from 3 for array 3 , the next element in the binary index tree contains arr[3] is 7. So how we determine this. Actually when we have 1xxxx01111, the next index is 1xxxx11111. Because of only 1...1contains previous value.

Next problem is how we write code for these. We can use x | (x + 1) to find the next element in the binary index tree.

Suppose we are start from 0, the next four element is 0 | 1 = 1, 1 | 2 = 3, 3 | 4 = 7 , 7 | 8 = 15 . If we start from 2, the next four element is 2 | 3 = 3 then as same as 0.

Implementation[^2]

show detail

``` cpp using namespace std; template class fenwick { public: vector fenw; int n; fenwick(int _n) : n(_n) { fenw.resize(n); } void modify(int x, T v) { while (x < n) { fenw[x] += v; x |= (x + 1); } } T get(int x) { T v{}; while (x >= 0) { v += fenw[x]; x = (x & (x + 1)) - 1; } return v; } }; ``` </details> ## Problem set 1. https://codeforces.com/contest/1616/problem/E [^1]: https://en.wikipedia.org/wiki/Fenwick_tree [^2]: template code is from tourist