2. Differentiable manifolds; tangent space

2.1 DEFINITION. A differentiable manifold of dimension $n$ is a set $M$ and a family of injective mappings $\mathbf{x}_\alpha: U_\alpha \subset \mathbb{R}^n \to M$ of open sets $U_\alpha$ of $\mathbb{R}^n$ into $M$ such that:

1. $\bigcup_\alpha \mathbf{x}_\alpha(U_\alpha) = M$ .
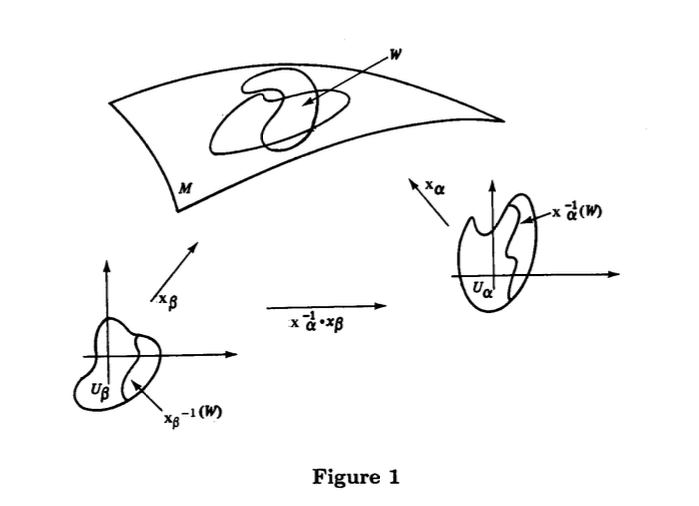
2. for any pair $\alpha, \beta$ , with $\mathbf{x}_\alpha(U_\alpha) \cap \mathbf{x}_\beta(U_\beta) = W \neq \emptyset$ , the sets $\mathbf{x}_\alpha^{-1}(W)$ and $\mathbf{x}_\beta^{-1}(W)$ are open sets in $\mathbb{R}^n$ and the mappings $\mathbf{x}_\beta^{-1} \circ \mathbf{x}_\alpha$ are differentiable (Fig. 1).
3. The family $\{ (U_\alpha, \mathbf{x}_\alpha) \}$ is maximal relative to the conditions (1) and (2).

The pair $(U_\alpha, \mathbf{x}_\alpha)$ (or the mapping $\mathbf{x}_\alpha$ ) with $p \in \mathbf{x}_\alpha(U_\alpha)$ is called a parametrization (or system of coordinates) of $M$ at $p$ ; $\mathbf{x}_\alpha(U_\alpha)$ is then called a coordinate neighborhood at $p$ . A family $\{ (U_\alpha, \mathbf{x}_\alpha) \}$ satisfying (1) and (2) is called a differentiable structure on $M$ .

The condition (3) is included for purely technical reasons. Indeed, given a differentiable structure on $M$ , we can easily complete it to a maximal one, by taking the union of all the parametrizations that, together with any of the parametrizations of the given structure, satisfy condition (2). Therefore, with a certain abuse of language, we can say that a differentiable manifold is a set provided with a differentiable structure. In general, the extension to the maximal structure will be done without further comment.

2.2 REMARK A comparison between the definition 2.1 and the definition of a regular surface in $\mathbb{R}^3$ shows that the essential point (except for the change of dimension from 2 to $n$ ) was to distinguish the fundamental property of the change of parameters (which is a theorem for surfaces in $\mathbb{R}^3$ ) and incorporate it as an axiom. This is precisely condition 2 of Definition 2.1. As we shall soon see, this is the condition that allows us to carry over all of the ideas of differential calculus in $\mathbb{R}^n$ to differentiable manifolds.

2.3 REMARK A differentiable structure on a set $M$ induces a natural topology on $M$ . It suffices to define $A \subset M$ to be an open set in $M$ if and only if $x_\alpha^{-1}(A \cap x_\alpha(U_\alpha))$ is an open set in $\mathbb{R}^n$ for all $\alpha$ . It is easy to verify that $M$ and the empty set are open sets, that a union of open sets is again an open set and that the finite intersection of open sets remains an open set. Observe that the topology is defined in such a way that the sets $x_\alpha(U_\alpha)$ are open and that the mappings $x_\alpha$ are continuous.

The Euclidean space $\mathbb{R}^n$ , with the differentiable structure

given by the identity, is a trivial example of a differentiable manifold. Now we shall see a non-trivial example.

2.4 EXAMPLE The real projective space $P^n(\mathbb{R})$ . Let us denote by $P^n(\mathbb{R})$ the set of straight lines of $\mathbb{R}^{n+1}$ which pass through the origin $0 = (0, \dots, 0) \in \mathbb{R}^{n+1}$ ; that is, $P^n(\mathbb{R})$ is the set of “directions” of $\mathbb{R}^{n+1}$ .

Let us introduce a differentiable structure on $P^n(\mathbb{R})$ . For this, let $(x_1, \dots, x_{n+1}) \in \mathbb{R}^{n+1}$ and observe, to begin with, that $P^n(\mathbb{R})$ is the quotient space of $\mathbb{R}^{n+1} - \{0\}$ by the equivalence relation:

The points of $P^n(\mathbb{R})$ will be denoted by $[x_1, \dots, x_{n+1}]$ . Observe that, if $x_i \neq 0$ ,

Define subsets $V_1, \dots, V_{n+1}$ , of $P^n(\mathbb{R})$ , by:

Geometrically, $V_i$ is the set of straight lines $\mathbb{R}^{n+1}$ which pass through the origin and do not belong to the hyperplane $x_i = 0$ . We are now going to show that we can take the $V_i$ ’s as coordinate neighborhoods, where the coordinates on $V_i$ are

For this, we will define mappings $\mathbf{x}_i: \mathbb{R}^n \to V_i$ by

and will show that the family $\{(\mathbb{R}^n, \mathbf{x}_i)\}$ is a differentiable structure on $P^n(\mathbb{R})$ .

Indeed, any mapping $\mathbf{x}_i$ is clearly bijective while $\bigcup \mathbf{x}_i(\mathbb{R}^n) = P^n(\mathbb{R})$ . It remains to show that $\mathbf{x}_i^{-1}(V_i \cap V_j)$ is an open set in

$\mathbb{R}^n$ and that $\mathbf{x}_j^{-1} \circ \mathbf{x}_i$ , $j = 1, \dots, n+1$ , is differentiable there. Now, if $i > j$ , the points in $\mathbf{x}_i^{-1}(V_i \cap V_j)$ are of the form:

Therefore $\mathbf{x}_i^{-1}(V_i \cap V_j)$ is an open set in $\mathbb{R}^n$ , and supposing that $i > j$ (the case $i < j$ is similar),

which is clearly differentiable.

In summary, the space of directions of $\mathbb{R}^{n+1}$ (real projective space $P^n(\mathbb{R})$ ) can be covered by $n+1$ coordinate neighborhoods $V_i$ , where the $V_i$ are made up of those directions of $\mathbb{R}^{n+1}$ that are not in the hyperplane $x_i = 0$ ; in addition, in each $V_i$ we have coordinates

where $(x_1, \dots, x_{n+1})$ are the coordinates of $\mathbb{R}^{n+1}$ . It is customary, in the classical terminology, to call the coordinates of $V_i$ “inhomogeneous coordinates” corresponding to the “homogeneous coordinates” $(x_1, \dots, x_{n+1}) \in \mathbb{R}^{n+1}$ .

Before presenting further examples of differentiable manifolds we should present a few more consequences of Definition 2.1. From now on, when we denote a differentiable manifold by $M^n$ , the upper index $n$ indicates the dimension of $M$ .

First, let us extend the idea of differentiability to mappings between manifolds.

2.5 DEFINITION. Let $M_1^n$ and $M_2^m$ be differentiable manifolds. A mapping $\varphi: M_1 \to M_2$ is differentiable at $p \in M_1$ if given a parametrization $\mathbf{y}: V \subset \mathbb{R}^n \to M_2$ at $\varphi(p)$ there exists a parametrization $\mathbf{x}: U \subset \mathbb{R}^n \to M_1$ at $p$ such that $\varphi(\mathbf{x}(U)) \subset \mathbf{y}(V)$ and the mapping

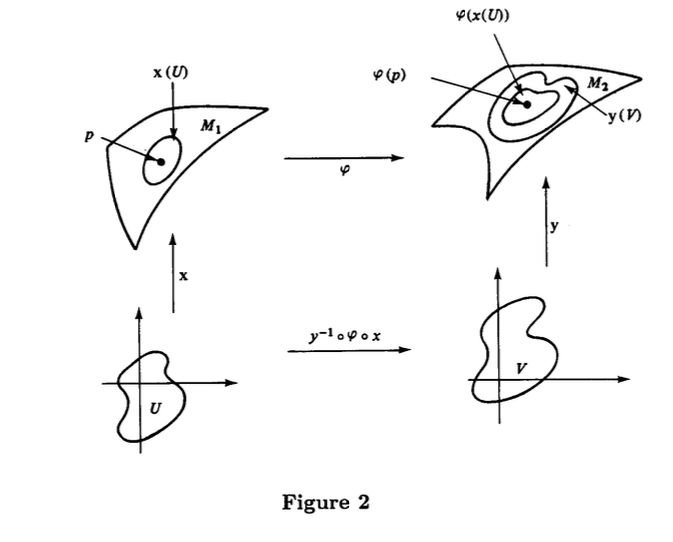
is differentiable at $x^{-1}(p)$ (Fig. 2). $\varphi$ is differentiable on an open set of $M_1$ if it is differentiable at all of the points of this open set.

It follows from condition (2) of Definition 2.1 that the given definition is independent of the choice of the parametrizations. The mapping (1) is called the expression of $\varphi$ in the parametrizations $x$ and $y$ .

Next, we would like to extend the idea of tangent vector to differentiable manifolds. It is convenient, as usual, to use our experience with regular surfaces in $\mathbb{R}^3$ . For surfaces in $\mathbb{R}^3$ , a tangent vector at a point $p$ of the surface is defined as the “velocity” in $\mathbb{R}^3$ of a curve in the surface passing through $p$ . Since we do not have at our disposal the support of the ambient space, we have to find a characteristic property of the tangent vector which will substitute for the idea of velocity.

The next considerations will motivate the definition that we

are going to present below. Let $\alpha: (-\varepsilon, \varepsilon) \to \mathbf{R}^n$ be a differentiable curve in $\mathbf{R}^n$ , with $\alpha(0) = p$ . Write

Then $\alpha'(0) = (x'_1(0), \dots, x'_n(0)) = v \in \mathbf{R}^n$ . Now let $f$ be a differentiable function defined in a neighborhood of $p$ . We can restrict $f$ to the curve $\alpha$ and express the directional derivative with respect to the vector $v \in \mathbf{R}^n$ as

Therefore, the directional derivative with respect to $v$ is an operator on differentiable functions that depends uniquely on $v$ . This is the characteristic property that we are going to use to define tangent vectors on a manifold.

2.6 DEFINITION. Let $M$ be a differentiable manifold. A differentiable function $\alpha: (-\varepsilon, \varepsilon) \to M$ is called a (differentiable) curve in $M$ . Suppose that $\alpha(0) = p \in M$ , and let $\mathcal{D}$ be the set of functions on $M$ that are differentiable at $p$ . The tangent vector to the curve $\alpha$ at $t=0$ is a function $\alpha'(0): \mathcal{D} \to \mathbf{R}$ given by

A tangent vector at $p$ is the tangent vector at $t=0$ of some curve $\alpha: (-\varepsilon, \varepsilon) \to M$ with $\alpha(0) = p$ . The set of all tangent vectors to $M$ at $p$ will be indicated by $T_p M$ .

If we choose a parametrization $\mathbf{x}: U \to M^n$ at $p = \mathbf{x}(0)$ , we can express the function $f$ and the curve $\alpha$ in this parametrization by

and

respectively. Therefore, restricting $f$ to $\alpha$ , we obtain

In other words, the vector $\alpha'(0)$ can be expressed in the parametrization $\mathbf{x}$ by

Observe that $\left( \frac{\partial}{\partial x_i} \right)_0$ is the tangent vector at $p$ of the “coordinate curve” (Fig. 3):

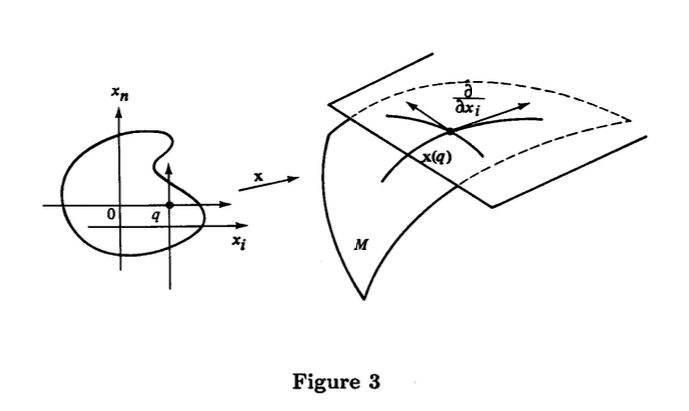
The expression (2) shows that the tangent vector to the curve $\alpha$ at $p$ depends only the derivative of $\alpha$ in a coordinate system. It follows also from (2) that the set $T_p M$ , with the usual operations of functions, forms a vector space of dimension $n$ , and that the choice of a parametrization $\mathbf{x}: U \to M$ determines an associated basis $\left\{ \left( \frac{\partial}{\partial x_1} \right)_0, \dots, \left( \frac{\partial}{\partial x_n} \right)_0 \right\}$ in $T_p M$ (Fig. 3). It is immediate that the linear structure in $T_p M$ defined above does not depend on the parametrization $\mathbf{x}$ . The vector space $T_p M$ is called the tangent space of $M$ at $p$ .

With the idea of tangent space we can extend to differentiable manifolds the notion of the differential of a differentiable mapping.

2.7 PROPOSITION. Let $M_1^n$ and $M_2^m$ be differentiable manifolds and let $\varphi: M_1 \to M_2$ be a differentiable mapping. For every $p \in M_1$ and for each $v \in T_p M_1$ , choose a differentiable curve $\alpha: (-\varepsilon, \varepsilon) \to M_1$ with $\alpha(0) = p$ , $\alpha'(0) = v$ . Take $\beta = \varphi \circ \alpha$ . The mapping $d\varphi_p: T_p M_1 \to T_{\varphi(p)} M_2$ given by $d\varphi_p(v) = \beta'(0)$ is a linear mapping that does not depend on the choice of $\alpha$ (Fig. 4).

Proof. Let $\mathbf{x}: U \to M_1$ and $\mathbf{y}: V \to M_2$ be parametrizations at $p$ and $\varphi(p)$ , respectively. Expressing $\varphi$ in these parametrizations, we can write

On the other hand, expressing $\alpha$ in the parametrization $\mathbf{x}$ , we obtain

Therefore,

It follows that the expression for $\beta'(0)$ with respect to the basis $\left\{ \left( \frac{\partial}{\partial y_i} \right)_0 \right\}$ of $T_{\varphi(p)} M_2$ , associated to the parametrization $\mathbf{y}$ , is given by

The relation (3) shows immediately that $\beta'(0)$ does not depend on the choice of $\alpha$ . In addition, (3) can be written as

where $\left( \frac{\partial y_i}{\partial x_j} \right)$ denotes an $m \times n$ matrix and $x'_j(0)$ denotes a column matrix with $n$ elements. Therefore, $d\varphi_p$ is a linear mapping of $T_p M_1$

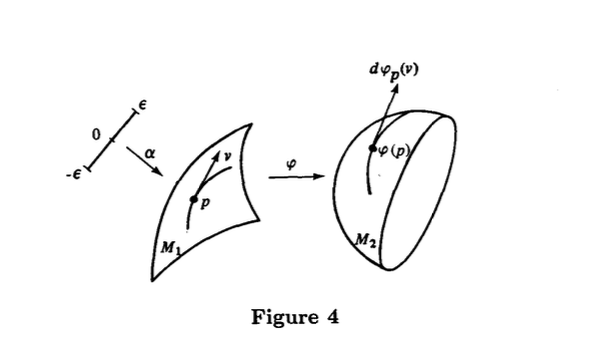
into $T_{\varphi(p)}M_2$ whose matrix in the associated bases obtained from the parametrizations $\mathbf{x}$ and $\mathbf{y}$ is precisely the matrix $\left(\frac{\partial y_i}{\partial x_j}\right)$ . $\square$

2.8 DEFINITION. The linear mapping $d\varphi_p$ defined by Proposition 2.7 is called the differential of $\varphi$ at $p$ .

2.9 DEFINITION. Let $M_1$ and $M_2$ be differentiable manifolds. A mapping $\varphi: M_1 \to M_2$ is a diffeomorphism if it is differentiable, bijective, and its inverse $\varphi^{-1}$ is differentiable. $\varphi$ is said to be a local diffeomorphism at $p \in M$ if there exist neighborhoods $U$ of $p$ and $V$ of $\varphi(p)$ such that $\varphi: U \to V$ is a diffeomorphism.

The notion of diffeomorphism is the natural idea of equivalence between differentiable manifolds. It is an immediate consequence of the chain rule that if $\varphi: M_1 \to M_2$ is a diffeomorphism, then $d\varphi_p: T_p M_1 \to T_{\varphi(p)} M_2$ is an isomorphism for all $p \in M_1$ ; in particular, the dimensions of $M_1$ and $M_2$ are equal. A local converse to this fact is the following theorem.

2.10 Theorem. Let $\varphi: M_1^n \to M_2^n$ be a differentiable mapping and let $p \in M_1$ be such that $d\varphi_p: T_p M_1 \to T_{\varphi(p)} M_2$ is an isomorphism. Then $\varphi$ is a local diffeomorphism at $p$ .

The proof follows from an immediate application of the inverse function theorem in $\mathbb{R}^n$ .