3. Immersions and embeddings; examples

3.1 DEFINITION Let $M^m$ and $N^n$ be differentiable manifolds. A differentiable mapping $\varphi: M \to N$ is said to be an immersion if $d\varphi_p: T_p M \to T_{\varphi(p)} N$ is injective for all $p \in M$ . If, in addition, $\varphi$ is a homeomorphism onto $\varphi(M) \subset N$ , where $\varphi(M)$ has the subspace topology induced from $N$ , we say that $\varphi$ is an embedding. If $M \subset N$ and the inclusion $i: M \subset N$ is an embedding, we say that $M$ is a submanifold of $N$ .

It can be seen that if $\varphi: M^m \to N^n$ is an immersion, then $m \le n$ ; the difference $n - m$ is called the codimension of the immersion $\varphi$ .

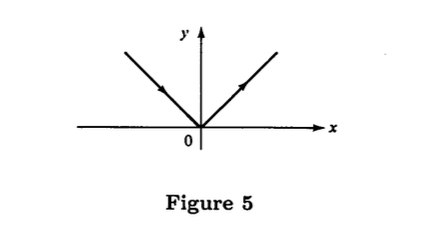
3.2 EXAMPLE The curve $\alpha: \mathbb{R} \to \mathbb{R}^2$ given by $\alpha(t) = (t, |t|)$ is not differentiable at $t = 0$ (Fig. 5).

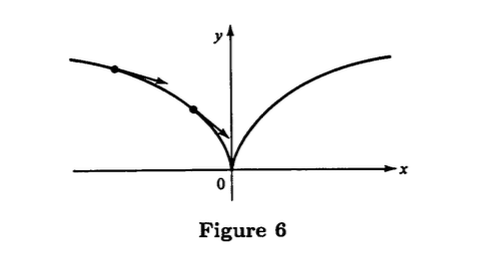
3.3 EXAMPLE The curve $\alpha: \mathbb{R} \to \mathbb{R}^2$ given by $\alpha(t) = (t^3, t^2)$ is a differentiable mapping but is not an immersion. Indeed, the condition for the map to be an immersion in this case is equivalent to the fact that $\alpha'(t) \neq 0$ , which does not occur for $t = 0$ (Fig. 6).

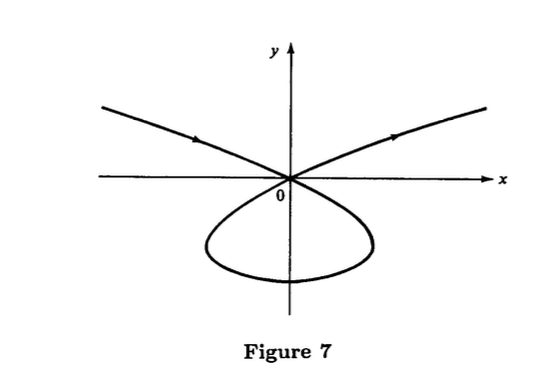
3.4 EXAMPLE The curve $\alpha(t) = (t^3 - 4t, t^2 - 4)$ (Fig. 7) is an immersion $\alpha: \mathbb{R} \to \mathbb{R}^2$ which has a self-intersection for $t = 2, t = -2$ . Therefore, $\alpha$ is not an embedding.

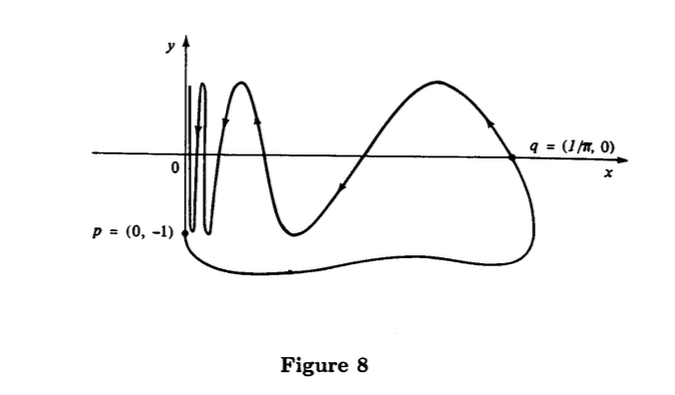
3.5 EXAMPLE The curve (Fig. 8)

is an immersion $\alpha: (-3, 0) \to \mathbb{R}^2$ without self-intersections. Nevertheless, $\alpha$ is not an embedding. Indeed, a neighborhood of a point $p$ , in the vertical part of the curve (Fig. 8) consists of an infinite number of connected components in the topology induced from $\mathbb{R}^2$ . On the other hand, a neighborhood of such a point in the topology “induced” from $\alpha$ (that is the topology of the line) is an open interval, hence a connected set.

3.6 EXAMPLE. It is clear that a regular surface $S \subset \mathbb{R}^3$ has a differentiable structure given by its parametrizations $\mathbf{x}_\alpha: U_\alpha \to S$ . With

such a structure, the mappings $\mathbf{x}_\alpha$ are differentiable and, indeed, are embeddings of $U_\alpha$ into $S$ ; that is an immediate consequence of conditions (a) and (b) of the definition of regular surface given in the introduction. We are going to show that the inclusion $i: S \subset \mathbf{R}^3$ is an embedding, that is, $S$ is a submanifold of $\mathbf{R}^3$ .

In fact, $i$ is differentiable, because for all $p \in S$ there exists a parametrization $\mathbf{x}: U \subset \mathbf{R}^2 \to S$ of $S$ at $p$ and a parametrization $j: V \subset \mathbf{R}^3 \to V$ of $\mathbf{R}^3$ at $i(p)$ ( $V$ is a neighborhood of $p$ in $\mathbf{R}^3$ and $j$ is the identity mapping), such that $j^{-1} \circ i \circ \mathbf{x} = \mathbf{x}$ is differentiable. In addition, from condition (b), $i$ is an immersion and, from condition (a), $i$ is a homeomorphism onto its image, which proves the claim.

For most local questions of geometry, it is the same to work with either immersions or embeddings. This comes from the following proposition which shows that every immersion is locally (in a certain sense) an embedding.

3.7 PROPOSITION Let $\varphi: M_1^n \to M_2^m$ , $n \le m$ , be an immersion of the differentiable manifold $M_1$ into the differentiable manifold $M_2$ . For every point $p \in M_1$ , there exists a neighborhood $V \subset M_1$ of $p$ such that the restriction $\varphi|_V: V \to M_2$ is an embedding.

Proof. This fact is a consequence of the inverse function theorem. Let $\mathbf{x}_1: U_1 \subset \mathbf{R}^n \to M_1$ and $\mathbf{x}_2: U_2 \subset \mathbf{R}^m \to M_2$ be a system

of coordinates at $p$ and at $\varphi(p)$ , respectively, and let us denote by $(x_1, \dots, x_n)$ the coordinates of $\mathbf{R}^n$ and by $(y_1, \dots, y_m)$ the coordinates of $\mathbf{R}^m$ . In these coordinates, the expression for $\varphi$ , that is, the mapping $\tilde{\varphi} = \mathbf{x}_2^{-1} \circ \varphi \circ \mathbf{x}_1$ , can be written

Let $q = \mathbf{x}_1^{-1}(p)$ . Since $\varphi$ is an immersion, we can suppose, renumbering the coordinates for both $\mathbf{R}^n$ and $\mathbf{R}^m$ , if necessary, that

To apply the inverse function theorem, we introduce the mapping $\phi = U_1 \times \mathbf{R}^{m-n=k} \to \mathbf{R}^m$ given by

where $(t_1, \dots, t_k) \in \mathbf{R}^{m-n=k}$ . It is easy to verify that $\phi$ restricted to $U_1$ coincides with $\tilde{\varphi}$ and that

It follows from the inverse function theorem, that there exist neighborhoods $W_1 \subset U_1 \times \mathbf{R}^k$ of $q$ and $W_2 \subset \mathbf{R}^m$ of $\phi(q)$ such that the restriction $\phi|_{W_1}$ is a diffeomorphism onto $W_2$ . Let $\tilde{V} = W_1 \cap U_1$ . Since $\phi|_{\tilde{V}} = \tilde{\varphi}|_{\tilde{V}}$ and $\mathbf{x}_i$ is a diffeomorphism, for $i = 1, 2$ , we conclude that the restriction to $V = \mathbf{x}_1(\tilde{V})$ of the mapping $\phi = \mathbf{x}_2 \circ \tilde{\varphi} \circ \mathbf{x}_1^{-1}: V \to \varphi(V) \subset M_2$ is a diffeomorphism, hence an embedding. $\square$