4. Other examples of manifolds. Orientation

4.1 EXAMPLE (The tangent bundle). Let $M^n$ be a differentiable manifold and let $TM = \{(p, v); p \in M, v \in T_p M\}$ . We are going to provide the set $TM$ with a differentiable structure (of dimension $2n$ ); with such a structure $TM$ will be called the tangent bundle of $M$ . This is the natural space to work with when treating questions that involve positions and velocities, as in the case of mechanics.

Let $\{(U_\alpha, \mathbf{x}_\alpha)\}$ be a maximal differentiable structure on $M$ . Denote by $(x_1^\alpha, \dots, x_n^\alpha)$ the coordinates of $U_\alpha$ and by $\left\{\frac{\partial}{\partial x_1^\alpha}, \dots, \frac{\partial}{\partial x_n^\alpha}\right\}$ the associated bases to the tangent spaces of $\mathbf{x}_\alpha(U_\alpha)$ . For every $\alpha$ , define

by

Geometrically, this means that we are taking as coordinates of a point $(p, v) \in TM$ the coordinates $x_1^\alpha, \dots, x_n^\alpha$ of $p$ together with the coordinates of $v$ in the basis $\left\{\frac{\partial}{\partial x_1^\alpha}, \dots, \frac{\partial}{\partial x_n^\alpha}\right\}$ .

We are going to show that $\{(U_\alpha \times \mathbf{R}^n, y_\alpha)\}$ is a differentiable structure on $TM$ . Since $\bigcup_\alpha \mathbf{x}_\alpha(U_\alpha) = M$ and $(d\mathbf{x}_\alpha)_q(\mathbf{R}^n) = T_{\mathbf{x}_\alpha(q)}M$ , $q \in U_\alpha$ , we have that

which verifies condition (1) of Definition 2.1. Now let

Then

where $q_\alpha \in U_\alpha$ , $q_\beta \in U_\beta$ , $v_\alpha, v_\beta \in \mathbf{R}^n$ . Therefore,

Since $x_\beta^{-1} \circ x_\alpha$ is differentiable, $d(x_\beta^{-1} \circ x_\alpha)$ is as well. It follows that $y_\beta^{-1} \circ y_\alpha$ is differentiable, which verifies condition (2) of the definition 2.1 and completes the example.

4.2 EXAMPLE. (Regular surfaces in $\mathbf{R}^n$ ). The natural generalization of the notion of a regular surface in $\mathbf{R}^3$ is the idea of a surface of dimension $k$ in $\mathbf{R}^n$ , $k \le n$ . A subset $M^k \subset \mathbf{R}^n$ is a regular surface of dimension $k$ if for every $p \in M^k$ there exists a neighborhood $V$ of $p$ in $\mathbf{R}^n$ and a mapping $x: U \subset \mathbf{R}^k \to M \cap V$ of an open set $U \subset \mathbf{R}^k$ onto $M \cap V$ such that:

1. $x$ is a differentiable homeomorphism.
2. $(dx)_q: \mathbf{R}^k \to \mathbf{R}^n$ is injective for all $q \in U$ .

Except for the dimensions involved, the definition is exactly the same as was given in the Introduction for a regular surface in $\mathbf{R}^3$ .

In a similar way as was done for surfaces in $\mathbf{R}^3$ (M. do Carmo [dC 2], p. 71), it can be proved that if $x: U \subset \mathbf{R}^k \to M^k$ and $y: V \subset \mathbf{R}^k \to M^k$ are two parametrizations with $x(U) \cap y(V) = W \neq \emptyset$ , then the mapping $h = x^{-1} \circ y: y^{-1}(W) \to x^{-1}(W)$ is a diffeomorphism. For completeness, we give a sketch of this proof in what follows.

First, we observe that $h$ is a homeomorphism, being a composition of homeomorphisms. Let $r \in y^{-1}(W)$ and put $q = h(r)$ . Let $(u_1, \dots, u_k) \in U$ and $(v_1, \dots, v_n) \in \mathbf{R}^n$ , and write $x$ in these coordinates as

From condition (b), we can suppose that

Extend $x$ to a mapping $F: U \times \mathbf{R}^{n-k} \to \mathbf{R}^n$ given by

where $(t_{k+1}, \dots, t_n) \in \mathbb{R}^{n-k}$ . It is clear that $F$ is differentiable and the restriction of $F$ to $U \times \{(0, \dots, 0)\}$ coincides with $x$ . By a simple calculation, we obtain that

We are then able to apply the inverse function theorem, which guarantees the existence of a neighborhood $Q$ of $x(q)$ where $F^{-1}$ exists and is differentiable. By the continuity of $y$ , there exists a neighborhood $R \subset V$ of $r$ such that $y(R) \subset Q$ . Note that the restriction of $h$ to $R$ , $h | R = F^{-1} \circ y | R$ is a composition of differentiable mappings. Thus $h$ is differentiable at $r$ , hence in $y^{-1}(W)$ . A similar argument would show that $h^{-1}$ is differentiable as well, proving the assertion. $\square$

From what we have just proved, it follows by an entirely similar argument as in Example 3.6 that $M^k$ is a differentiable manifold of dimension $k$ and that the inclusion $i: M^k \subset \mathbb{R}^n$ is an embedding, that is, $M^k$ is a submanifold of $\mathbb{R}^n$ .

4.3 EXAMPLE (Inverse image of a regular value). Before discussing the next example, we need some definitions.

Let $F: U \subset \mathbb{R}^n \to \mathbb{R}^m$ be a differentiable mapping of an open set $U$ of $\mathbb{R}^n$ . A point $p \in U$ is defined to be a critical point of $F$ if the differential $dF_p: \mathbb{R}^n \to \mathbb{R}^m$ is not surjective. The image $F(p)$ of a critical point is called a critical value of $F$ . A point $a \in \mathbb{R}^m$ that is not a critical value is said to be a regular value of $F$ . Note that any point $a \notin F(U)$ is trivially a regular value of $F$ and that if there exists a regular value of $F$ in $\mathbb{R}^m$ , then $n \ge m$ .

Now let $a \in F(U)$ be a regular value of $F$ . We are going to show that the inverse image $F^{-1}(a) \subset \mathbb{R}^n$ is a regular surface of dimension $n-m=k$ . From what was seen in Example 4.2, $F^{-1}(a)$ is then a submanifold of $\mathbb{R}^n$ .

To prove the assertion we use, again, the inverse function theorem. Let $p \in F^{-1}(a)$ . Denote by $q = (y_1, \dots, y_m, x_1, \dots, x_k)$ an arbitrary point of $\mathbb{R}^{n=m+k}$ and by $F(q) = (f_1(q), \dots, f_m(q))$ its image by the mapping $F$ . Since $a$ is a regular value of $F$ , $dF_p$ is surjective. Therefore, we can suppose that

Define a mapping $\varphi: U \subset \mathbb{R}^n \to \mathbb{R}^{n=m+k}$ by

Then

By the inverse function theorem, $\varphi$ is a diffeomorphism of a neighborhood $Q$ of $p$ onto a neighborhood $W$ of $\varphi(p)$ . Let $K^{m+k} \subset W \subset \mathbb{R}^{m+k}$ be a cube of center $\varphi(p)$ and put $V = \varphi^{-1}(K^{m+k}) \cap Q$ . Then $\varphi$ maps the neighborhood $V$ diffeomorphically onto $K^{m+k} = K^m \times K^k$ . Define a mapping $\mathbf{x}: K^k \to V$ by

where $(a_1, \dots, a_m) = a$ . It is easy to check that $\varphi$ satisfies conditions (a) and (b) of the definition of regular surface given in Example 4.2. Since $p$ is arbitrary, $F^{-1}(a)$ is a regular surface in $\mathbb{R}^n$ , as asserted.

Before going on to other examples of differentiable manifolds, we should introduce the important global notion of orientation.

4.4 DEFINITION Let $M$ be a differentiable manifold. We say that $M$ is orientable if $M$ admits a differentiable structure $\{(U_\alpha, \mathbf{x}_\alpha)\}$ such that:

(i) for every pair $\alpha, \beta$ , with $\mathbf{x}_\alpha(U_\alpha) \cap \mathbf{x}_\beta(U_\beta) = W \neq \emptyset$ , the differential of the change of coordinates $\mathbf{x}_\beta^{-1} \circ \mathbf{x}_\alpha$ has positive determinant.

In the opposite case, we say that $M$ is non-orientable. If $M$ is orientable, a choice of a differentiable structure satisfying (i) is called an orientation of $M$ . $M$ is then said to be oriented. Two differentiable structures that satisfy (i) determine the same orientation if their union again satisfies (i).

It is not difficult to verify that if $M$ is orientable and connected there exist exactly two distinct orientations on $M$ .

Now let $M_1$ and $M_2$ be differentiable manifolds and let $\varphi: M_1 \to M_2$ be a diffeomorphism. It is easy to verify that $M_1$ is orientable if and only if $M_2$ is orientable. If, additionally, $M_1$ and $M_2$ are connected and are oriented, $\varphi$ induces an orientation on $M_2$ which may or may not coincide with the initial orientation of $M_2$ . In the first case, we say that $\varphi$ preserves the orientation and in the second case, that $\varphi$ reverses the orientation.

4.5 EXAMPLE If $M$ can be covered by two coordinate neighborhoods $V_1$ and $V_2$ in such a way that the intersection $V_1 \cap V_2$ is connected, then $M$ is orientable. Indeed, since the determinant of the differential of the coordinate change is $\neq 0$ , it does not change sign in $V_1 \cap V_2$ ; if it is negative at a single point, it suffices to change the sign of one of the coordinates to make it positive at that point, hence on $V_1 \cap V_2$ .

4.6 EXAMPLE. The simple criterion of the previous example can be used to show that the sphere

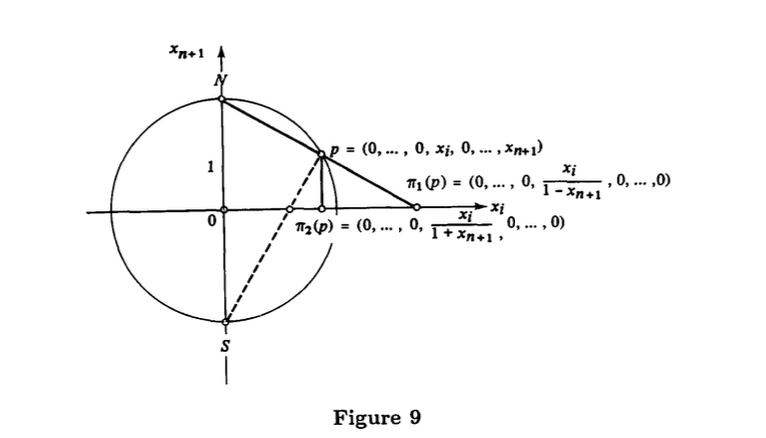
is orientable. Indeed, let $N = (0, \dots, 0, 1)$ be the north pole and $S = (0, \dots, 0, -1)$ the south pole of $S^n$ . Define a mapping $\pi_1: S^n - \{N\} \to \mathbf{R}^n$ (stereographic projection from the north pole) that takes $p = (x_1, \dots, x_{n+1})$ in $S^n - \{N\}$ into the intersection of the hyperplane $x_{n+1} = 0$ with the line that passes through $p$ and $N$ . It is easy to verify that (Fig. 9)

The mapping $\pi_1$ is differentiable, injective and maps $S^n - \{N\}$ onto the hyperplane $x_{n+1} = 0$ . The stereographic projection $\pi_2: S^n - \{S\} \to \mathbf{R}^n$ from the south pole onto the hyperplane $x_{n+1} = 0$ has the same properties.

Therefore, the parametrizations $(\mathbf{R}^n, \pi_1^{-1})$ , $(\mathbf{R}^n, \pi_2^{-1})$ cover $S^n$ . In addition, the change of coordinates:

is given by

(here we use the fact that $\sum_{k=1}^{n+1} x_k^2 = 1$ ). Therefore, the family $\{(\mathbf{R}^n, \pi_1^{-1}), (\mathbf{R}^n, \pi_2^{-1})\}$ is a differentiable structure on $S^n$ . Observe that the intersection $\pi_1^{-1}(\mathbf{R}^n) \cap \pi_2^{-1}(\mathbf{R}^n) = S^n - \{N \cup S\}$ is connected, thus $S^n$ is orientable and the family given determines an orientation of $S^n$ .

A diagram illustrating the stereographic projection from the unit sphere $S^n$ (represented by a circle) onto the plane $\mathbb{R}^n$ (represented by the horizontal axis). The vertical axis is labeled $x_{n+1}$ . The origin is labeled 0, and the top point is labeled N (North pole). The bottom point is labeled S (South pole). A point $p$ on the sphere is shown, with coordinates $p = (0, \dots, 0, x_i, 0, \dots, x_{n+1})$ . The projection $\pi_1(p)$ is shown on the positive $x_i$ axis, with coordinates $\pi_1(p) = (0, \dots, 0, \frac{x_i}{1-x_{n+1}}, 0, \dots, 0)$ . The projection $\pi_2(p)$ is shown on the negative $x_i$ axis, with coordinates $\pi_2(p) = (0, \dots, 0, \frac{x_i}{1+x_{n+1}}, 0, \dots, 0)$ .

Now let $A: S^n \to S^n$ be the antipodal map given by $A(p) = -p$ , $p \in \mathbb{R}^{n+1}$ . $A$ is differentiable and $A^2 = \text{ident}$ . Therefore, $A$ is a diffeomorphism of $S^n$ . Observe that when $n$ is even, $A$ reverses the orientation of $S^n$ and when $n$ is odd, $A$ preserves the orientation of $S^n$ .

We are now in a position to exhibit some other examples of differentiable manifolds.

4.7 EXAMPLE. (Another description of projective space). The set $P^n(\mathbb{R})$ of lines of $\mathbb{R}^{n+1}$ that pass through the origin can be thought of as the quotient space of the unit sphere $S^n = \{p \in \mathbb{R}^{n+1}; |p| = 1\}$ by the equivalence relation that identifies $p \in S^n$ with its antipodal point, $A(p) = -p$ . Indeed, each line that passes through the origin determines two antipodal points and the correspondence so obtained is evidently bijective.

Taking into account this fact, we are going to introduce another differentiable structure on $P^n(\mathbb{R})$ (Cf. Example 2.4). For this, we initially introduce on $S^n \subset \mathbb{R}^{n+1}$ the structure of a regular surface, defining parametrizations

in the following way:

where $D_i = \sqrt{1 - (x_1^2 + \dots + x_{i-1}^2 + x_{i+1}^2 + \dots + x_{n+1}^2)}$ . It is easy to verify that conditions (a) and (b) of the definition in Example 4.2 are satisfied. Therefore, the family

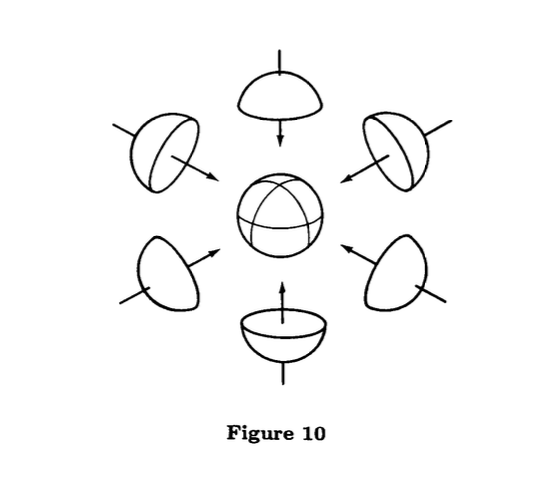
is a differentiable structure on $S^n$ . Geometrically, this is equivalent to covering the sphere $S^n$ with coordinate neighborhoods that are hemi-spheres perpendicular to the axes $x_i$ and taking as coordinates on, for example, $\mathbf{x}_i^+(U_i)$ , the coordinates of the orthogonal projection of $\mathbf{x}_i^+(U_i)$ on the hyperplane $x_i = 0$ (Fig. 10).

Let $\pi: S^n \to P^n(\mathbb{R})$ be the canonical projection, that is, $\pi(p) = \{p, -p\}$ ; observe that $\pi(x_i^+(U_i)) = \pi(x_i^-(U_i))$ . We are going to define a mapping $y_i: U_i \to P^n(\mathbb{R})$ by

Since $\pi$ restricted to $x_i^+(U_i)$ is one-to-one, we have that

which yields the differentiability of $y_i^{-1} \circ y_j$ , for all $i, j = 1, \dots, n+1$ . Thus the family $\{(U_i, y_i)\}$ is a differentiable structure for $P^n(\mathbb{R})$ .

In fact, this differentiable structure and that of Example 2.4 give rise to the same maximal structure. Indeed, the coordinate neighborhoods are the same and the change of coordinates are given by:

which, since $x_i \neq 0$ and $D_i \neq 0$ , is differentiable.

As we shall see in Exercise 9, $P^n(\mathbb{R})$ is orientable if and only if $n$ is odd.

4.8 EXAMPLE (Discontinuous action of a group). There is a way of constructing differentiable manifolds that generalizes the process above, which is given by the following considerations.

We say that a group $G$ acts on a differentiable manifold $M$ if there exists a mapping $\varphi: G \times M \to M$ such that:

1. For each $g \in G$ , the mapping $\varphi_g: M \to M$ given by $\varphi_g(p) = \varphi(g, p)$ , $p \in M$ , is a diffeomorphism, and $\varphi_e = \text{identity}$ .
2. If $g_1, g_2 \in G$ , $\varphi_{g_1 g_2} = \varphi_{g_1} \circ \varphi_{g_2}$ .

Frequently, when dealing with a single action, we set $\varphi(g, p) = gp$ ; in this notation, condition (ii) can be interpreted as a form of associativity: $(g_1 g_2)p = g_1(g_2 p)$ .

We say that the action is properly discontinuous if every $p \in M$ has a neighborhood $U \subset M$ such that $U \cap g(U) = \emptyset$ for all $g \neq e$ .

When $G$ acts on $M$ , the action determines an equivalence relation $\sim$ on $M$ , in which $p_1 \sim p_2$ if and only if $p_2 = gp_1$ , for some

$g \in G$ . Denote the quotient space of $M$ by this equivalence relation by $M/G$ . The mapping $\pi: M \to M/G$ , given by

will be called the projection of $M$ onto $M/G$ .

Now let $M$ be a differentiable manifold and let $G \times M \to M$ be a properly discontinuous action of a group $G$ on $M$ . We are going to show that $M/G$ has a differentiable structure with respect to which the projection $\pi: M \to M/G$ is a local diffeomorphism.

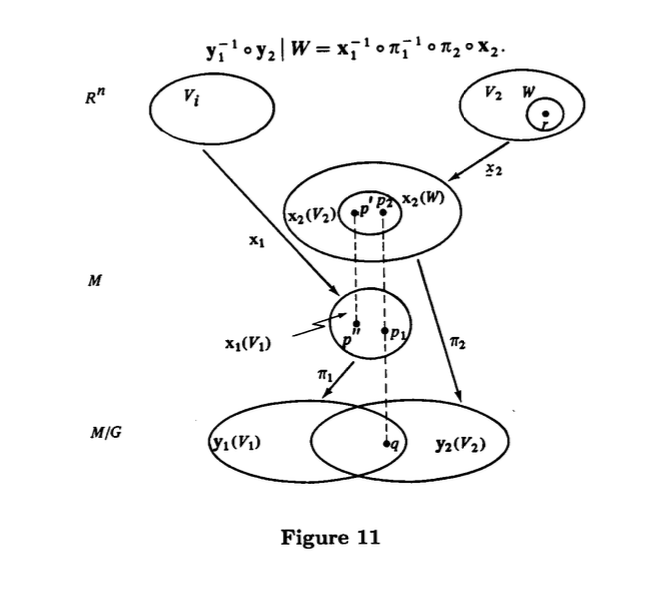
For each $p \in M$ choose a parametrization $\mathbf{x}: V \to M$ at $p$ so that $\mathbf{x}(V) \subset U$ , where $U \subset M$ is a neighborhood of $p$ such that $U \cap g(U) = \emptyset$ , $g \neq e$ . Clearly $\pi|_U$ is injective, hence $y = \pi \circ \mathbf{x}: V \to M/G$ is injective. The family $\{(V, y)\}$ clearly covers $M/G$ ; for such a family to be a differentiable structure, it suffices to show that given two mappings $y_1 = \pi \circ \mathbf{x}_1: V_1 \to M/G$ and $y_2 = \pi \circ \mathbf{x}_2: V_2 \to M/G$ with $y_1(V_1) \cap y_2(V_2) \neq \emptyset$ , then $y_1^{-1} \circ y_2$ is differentiable.

For this, let $\pi_i$ be the restriction of $\pi$ to $x_i(V_i)$ , $i = 1, 2$ . Let $q \in y_1(V_1) \cap y_2(V_2)$ and let $r = \mathbf{x}_2^{-1} \circ \pi_2^{-1}(q)$ . Let $W \subset V_2$ be a neighborhood of $r$ such that $(\pi_2 \circ \mathbf{x}_2)(W) \subset y_1(V_1) \cap y_2(V_2)$ (Fig. 11). Then, the restriction to $W$ is given by

Therefore, it is enough to show that $\pi_1^{-1} \circ \pi_2$ is differentiable at $p_2 = \pi_2^{-1}(q)$ . Let $p_1 = \pi_1^{-1} \circ \pi_2(p_2)$ . Then $p_1$ and $p_2$ are equivalent in $M$ , hence there is a $g \in G$ such that $gp_2 = p_1$ . It follows easily that the restriction $\pi_1^{-1} \circ \pi_2 | \mathbf{x}_2(W)$ coincides with the diffeomorphism $\varphi_g | \mathbf{x}_2(W)$ , which proves that $\pi_1^{-1} \circ \pi_2$ is differentiable at $p_2$ , as stated.

From the very way in which this differentiable structure is constructed, $\pi: M \to M/G$ is a local diffeomorphism. A criterion for the orientability of $M/G$ is given in Exercise 9. Observe that the situation in the previous example reduces to the present one, by taking $M = S^n$ and $G$ the group of diffeomorphisms of $S^n$ formed by the antipodal mapping $A$ and the identity $I = A^2$ of $S^n$ .

4.9 EXAMPLE (special cases of Example 4.8).

4.9 (a). Consider the group $G$ of “integral” translations of $\mathbb{R}^k$ where the action of $G$ on $\mathbb{R}^k$ is given by

$y_1^{-1} \circ y_2 | W = x_1^{-1} \circ \pi_1^{-1} \circ \pi_2 \circ x_2.$

Diagram illustrating the relationship between coordinate charts $V_1$ and $V_2$ on $R^n$ , their images $x_1(V_1)$ and $x_2(V_2)$ on $M$ , and their images $y_1(V_1)$ and $y_2(V_2)$ on $M/G$ . The diagram shows the overlap region $x_2(V_2) \cap x_1(V_1)$ on $M$ and the corresponding overlap region $y_2(V_2) \cap y_1(V_1)$ on $M/G$ . The mapping $y_1^{-1} \circ y_2$ is defined on the overlap region $W$ of $y_1(V_1)$ and $y_2(V_2)$ on $M/G$ . The relationship between the coordinates is given by the equation above.

It is easy to check that the mapping above defines an action of $G$ on $\mathbb{R}^k$ , which is properly discontinuous. The quotient space $\mathbb{R}^k/G$ , with the differentiable structure described in Example 4.8, is called the $k$ -torus $T^k$ . When $k=2$ , the 2-torus $T^2$ is diffeomorphic to the torus of revolution in $\mathbb{R}^3$ obtained as the inverse image of zero of the function $f: \mathbb{R}^3 \to \mathbb{R}$

(Cf. M. do Carmo [dC 2], p. 62).

4.9 (b). Let $S \subset \mathbb{R}^3$ be a regular surface in $\mathbb{R}^3$ , symmetric relative to the origin $0 \in \mathbb{R}^3$ , that is, if $p \in S$ then $-p = A(p) \in S$ . The group of diffeomorphisms of $S$ formed by $\{A, Id.\}$ acts on $S$ in a properly discontinuous manner. Introduce on $S/G$ the differentiable structure given by Example 4.8. When $S$ is the torus of revolution $T^2$ , $S/G = K$ is called the Klein bottle; when $S$ is the right circular cylinder given by $C = \{(x, y, z) \in \mathbb{R}^3; x^2 + y^2 = 1, -1 < z < 1\}$ , $S/G$ is called the Möbius band. As we shall see in Exercise 9, the Klein bottle and the Möbius band are non-orientable. In Exercise 6, we shall indicate how the Klein bottle can be embedded in $\mathbb{R}^4$ .