树状数组
背景
芬威克树(Fenwick tree) 或 树状数组(binary indexed tree) 是一种数据结构,可以高效地更新元素和计算数字表中的前缀和。[^1]
空间和时间复杂度
解释
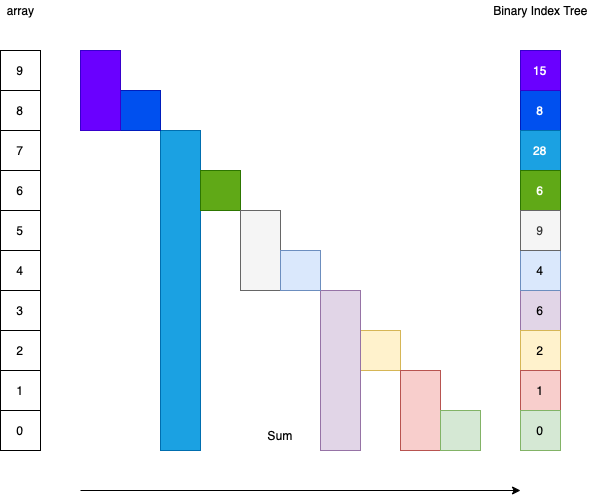
上图显示了存储在树状数组中的数据。
假设原始数组的名称是 arr,树状数组的名称是 fenw。那么 arr 和 fenw 之间有以下关系。
fenw[0] = arr[0];
fenw[1] = arr[0] + arr[1];
fenw[2] = arr[2];
fenw[3] = arr[0] + arr[1] + arr[2] + arr[3];现在,我们需要找到规律。首先,我们要找出 fenw 中所有包含 arr[0] 的索引。这些索引是 0, 1, 3, 7, 15, ...。现在我们看到了 arr[0] 的规律。第一个是 0;第二个是 1,即 0 + 1 = 0 + 2^0;第三个是 3,即 1 + 2^1 = 3,依此类推。当我们从索引 3 开始时,树状数组中下一个包含 arr[3] 的元素在索引7处。那么我们如何确定这一点呢?要获取下一个索引,我们可以使用公式 index | (index + 1)。这是通过将最低有效零位翻转为一来实现的。
下一个问题是如何为此编写代码。我们可以使用 x | (x + 1) 来找到树状数组中的下一个元素。
假设我们从 0 开始。接下来的四个元素是 0 | (0 + 1) = 1,1 | (1 + 1) = 3,3 | (3 + 1) = 7,7 | (7 + 1) = 15。如果我们从 2 开始,下一个元素是 2 | (2 + 1) = 3,然后它遵循与从0开始相同的模式。
实现[^2]
显示细节
``` cpp using namespace std;template
fenwick(int _n) : n(_n) { fenw.resize(n); }
void modify(int x, T v) { while (x < n) { fenw[x] += v; x |= (x + 1); } }
T get(int x) { T v{}; while (x >= 0) { v += fenw[x]; x = (x & (x + 1)) - 1; } return v; } };
</details>
## 问题集
1. https://codeforces.com/contest/1616/problem/E
[^1]: https://en.wikipedia.org/wiki/Fenwick_tree
[^2]: 模板代码来自 tourist