Blogs
Binary indexed tree

Binary indexed tree

October 4, 2023

Background

A Fenwick tree or binary indexed tree is a data structure that can efficiently update elements and calculate prefix sums in a table of numbers.[^1]

Space and Time Complexity

 Algorithm  Average  Worst case  Space O(n)O(n) Search O(log⁡n)O(log⁡n) Insert O(log⁡n)O(log⁡n) Delete O(log⁡n)O(log⁡n) \begin{array}{lll} \text { Algorithm } & \text { Average } & \text { Worst case } \\ \text { Space } & \mathrm{O}(n) & \mathrm{O}(n) \\ \text { Search } & \mathrm{O}(\log n) & \mathrm{O}(\log n) \\ \text { Insert } & \mathrm{O}(\log n) & \mathrm{O}(\log n) \\ \text { Delete } & \mathrm{O}(\log n) & \mathrm{O}(\log n) \end{array}

Explanation

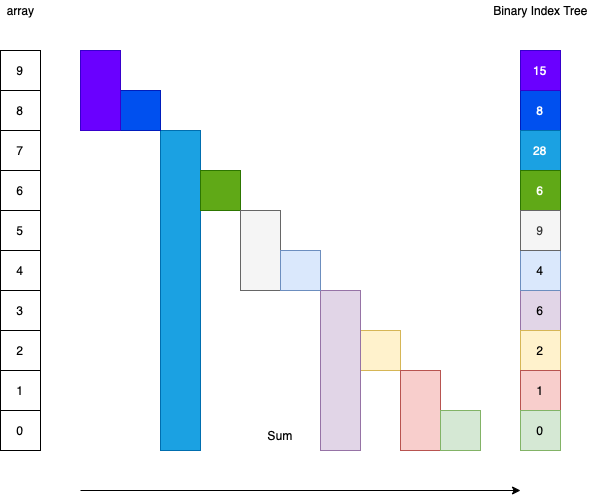
image-20220208141125368

The picture shows the data stored in the binary indexed tree.

Suppose the name of the original array is arr and the name of the binary indexed tree is fenw. Then we have the following relationship between arr and fenw.

fenw[0] = arr[0];
fenw[1] = arr[0] + arr[1];
fenw[2] = arr[2];
fenw[3] = arr[0] + arr[1] + arr[2] + arr[3];

Now, we need to find the pattern. First, we are going to find out all indices in fenw that contain arr[0]. The indices are 0, 1, 3, 7, 15, ... . Now we see the pattern for arr[0]. The first one is 0; the second one is 1, which is 0 + 1 = 0 + 2^0; the third one is 3, which is 1 + 2^1 = 3, and so on. When we are starting from index 3, the next element in the binary indexed tree that contains arr[3] is at index 7. So how do we determine this? To get the next index, we can use the formula index | (index + 1). This works by flipping the least significant zero bit to a one.

The next problem is how to write code for this. We can use x | (x + 1) to find the next element in the binary index tree.

Suppose we start from 0. The next four elements are 0 | (0 + 1) = 1, 1 | (1 + 1) = 3, 3 | (3 + 1) = 7, 7 | (7 + 1) = 15 . If we start from 2, the next element is 2 | (2 + 1) = 3, and from there it follows the same pattern as starting from 0.

Implementation[^2]

Show Detail``` cpp using namespace std;

template class fenwick { public: vector fenw; int n;

fenwick(int _n) : n(_n) { fenw.resize(n); }

void modify(int x, T v) { while (x < n) { fenw[x] += v; x |= (x + 1); } }

T get(int x) { T v{}; while (x >= 0) { v += fenw[x]; x = (x & (x + 1)) - 1; } return v; } };

</details>



## Problem set

1. https://codeforces.com/contest/1616/problem/E



[^1]: https://en.wikipedia.org/wiki/Fenwick_tree 
[^2]: template code is from tourist
Image to image translationNatural Language Processing